身近に潜む数学たち

2023/06/13

みなさんこんにちは！

本日のブログを担当する担任助手の佐藤です。

今日の内容はいつもと少し変わって身近に潜むいろいろな数学のお話を少ししたいと思います…が！数式を使った難しい話は出てきません。そんなところにも数学があるんだなぁくらいの気持ちで読んでいただければ幸いです。

高校数学を勉強している人なら見たことのある媒介変数であらわされた式の”概形を求めよ”なんて問題を解いたことがある人も多いのではないでしょうか？微分して増減表をつくって矢印を書いて…なんてことをしますよね。でも、パソコンを使って大量の変数を代入することで計算せずとも概形を求めることができちゃいます。

例えば

のようになります。右側に図形を作る式を載せていますが深くは考えなくて大丈夫です。ここではもう少しいろいろな媒介変数であらわされた図形を描かせてみましょう。

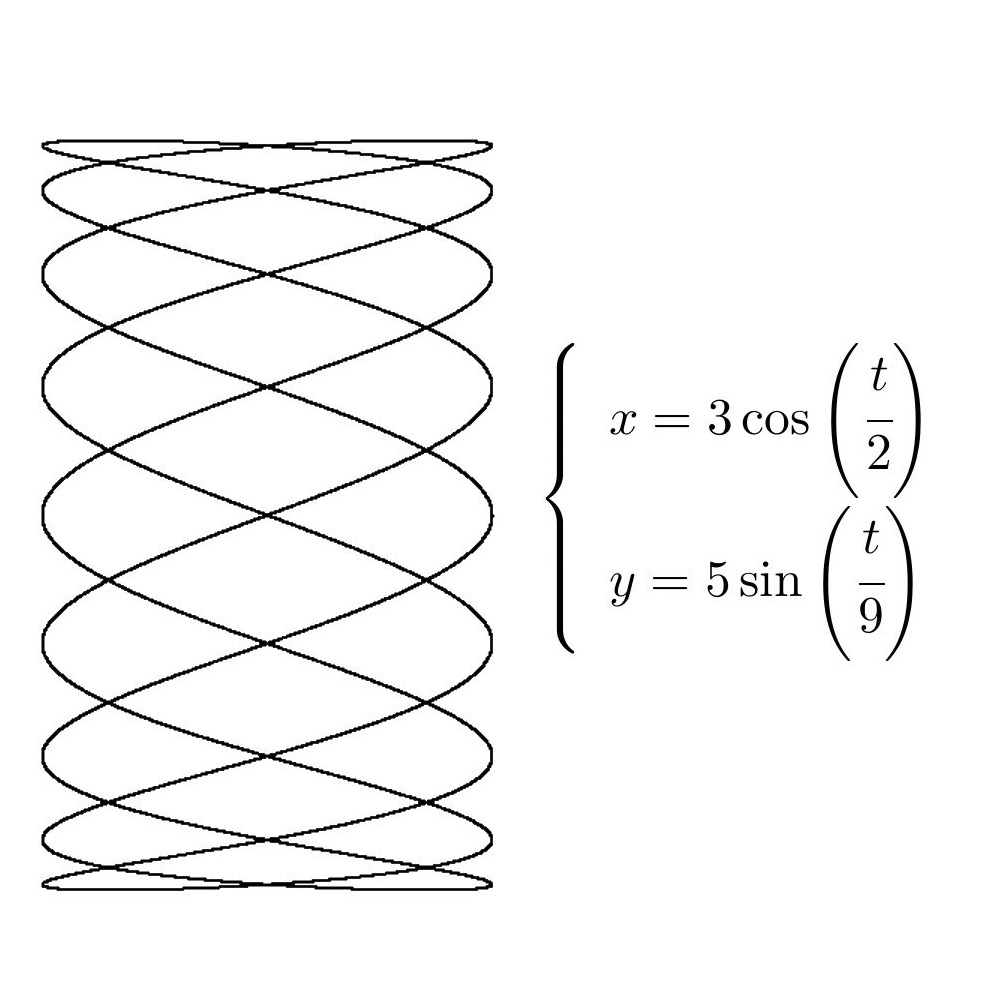
これはアップルパイを上から見たようなリサージュ曲線といわれるものです。がアップルパイと深い関係がある訳ではありません。おいしそうですね。

これは対数らせんと呼ばれ銀河から巻貝まで様々な形に現れるらせんです。別名等角らせんとも呼ばれており、曲線のどの位置から見ても線に対して中心が同じ方向に見え続けるためです。例えばゴールに向かってまっすぐ走らずつねに左前の同じ場所に見えるように走れば対数らせんを自然と描くということです。意外と作り方がシンプルで、自然に出てきそうな感じがしますね。

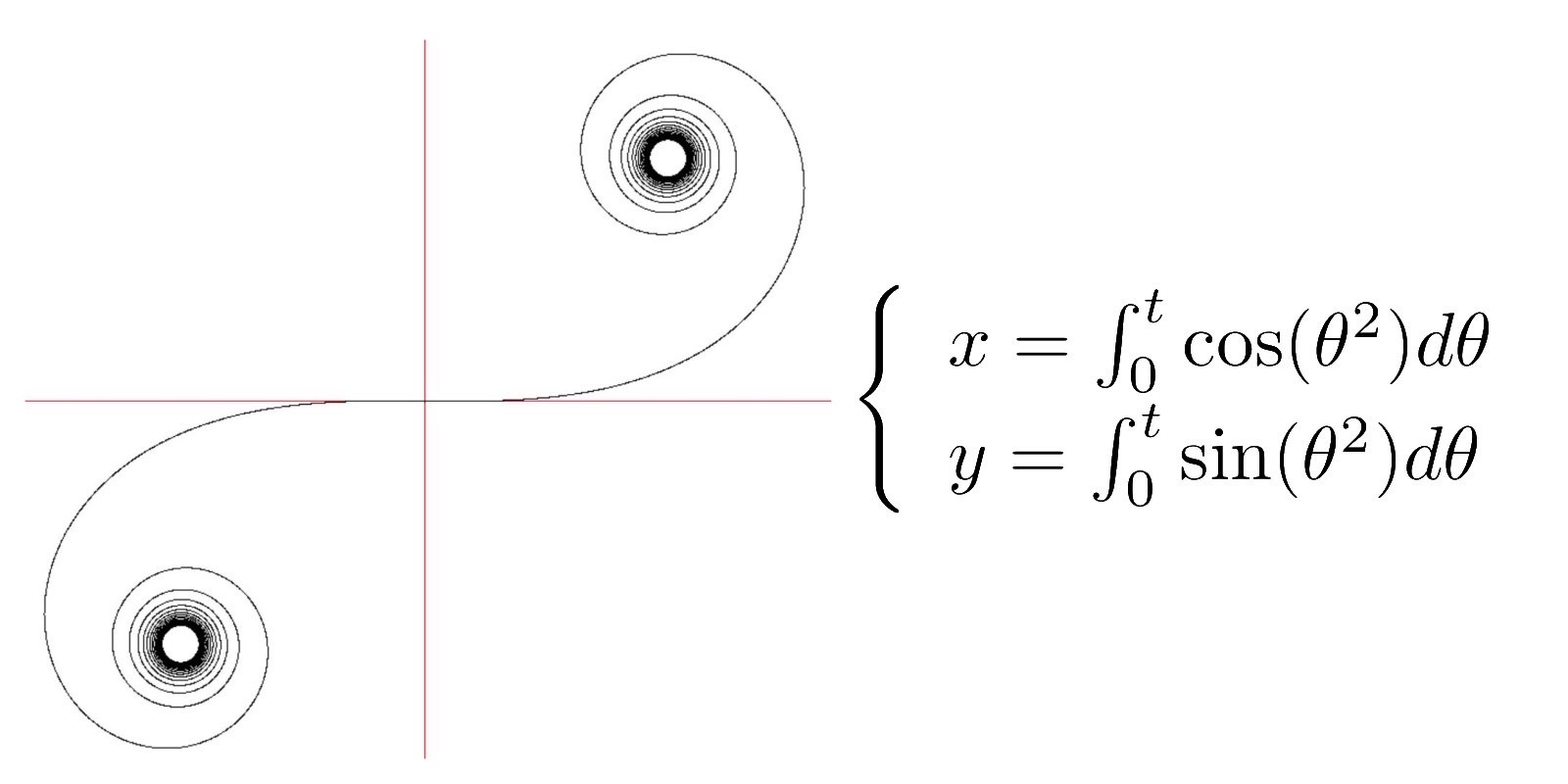
これはクロソイドと呼ばれるらせんです。このらせんは緩和曲線の一種であり、身近なところでよく使われています。いったい何を緩和してくれるのか…というと乗り心地です。少しだけ物理の話になりますがカーブを走っていると遠心力を感じますよね。

この力は半径の二乗に反比例—つまり半径が小さいほど強い力がかかります。高速道路を走っていてカーブがきれいな円だったとするとカーブに入るや否や一気に遠心力がかかります。

それはカーブに入ると急にある値の半径の道になるためです。そしてハンドルもこの円に合わせてこれまた一気に曲げなければ車線から出てしまいます。そうなってしまうと急な遠心力がかかる中で急ハンドルという事故まっしぐらな運転をしなければならなくなってしまいます。それを防ぐためのカーブこそこのクロソイドです。この曲線は半径が無限の円の一部ともとれる直線から徐々に半径が小さくなる円をつなげていったような形をしているので、クロソイドで作られた道路では曲がるときにかかる遠心力は少しずつ大きくなっていき、ハンドルもゆっくり回せばいいという先ほどの問題を解決した道路になります。さらにクロソイドの仲間の緩和曲線にはスマートフォンのアプリの角の取れた四角いアイコンの形にも使われており、丸よりも丸みのあるアイコンによる見た時の美しさを追及しています。

どうでしたか？実は身の回りにこんなにもいろいろな数学が潜んでいることを知って、数学の面白さが少しでも伝われば幸いです。弁天町駅前校ではこのような面白さを語り合える担任助手(スタッフ)もたくさん在籍しています。自分の好きな科目の面白さについて一緒に深めていきませんか？

―――――――――――――――――――――――――――――――――――――――――――――――――――

☆下記イベントは全て無料招待☆

【東進を知りたい！】

『一日体験』申込み受付中！！

対象学年：高１生，高２生，高３生

【部活と勉強を両立させたい！引退後の勉強計画も全力サポート！】

『部活生招待講習』申込み受付中！！

対象学年：高３生

【受験勉強を本格スタート！】

『夏期特別招待講習』申込み受付中

対象学年：高０生，高１生，高２生，高３生